Metcalfe’s Law
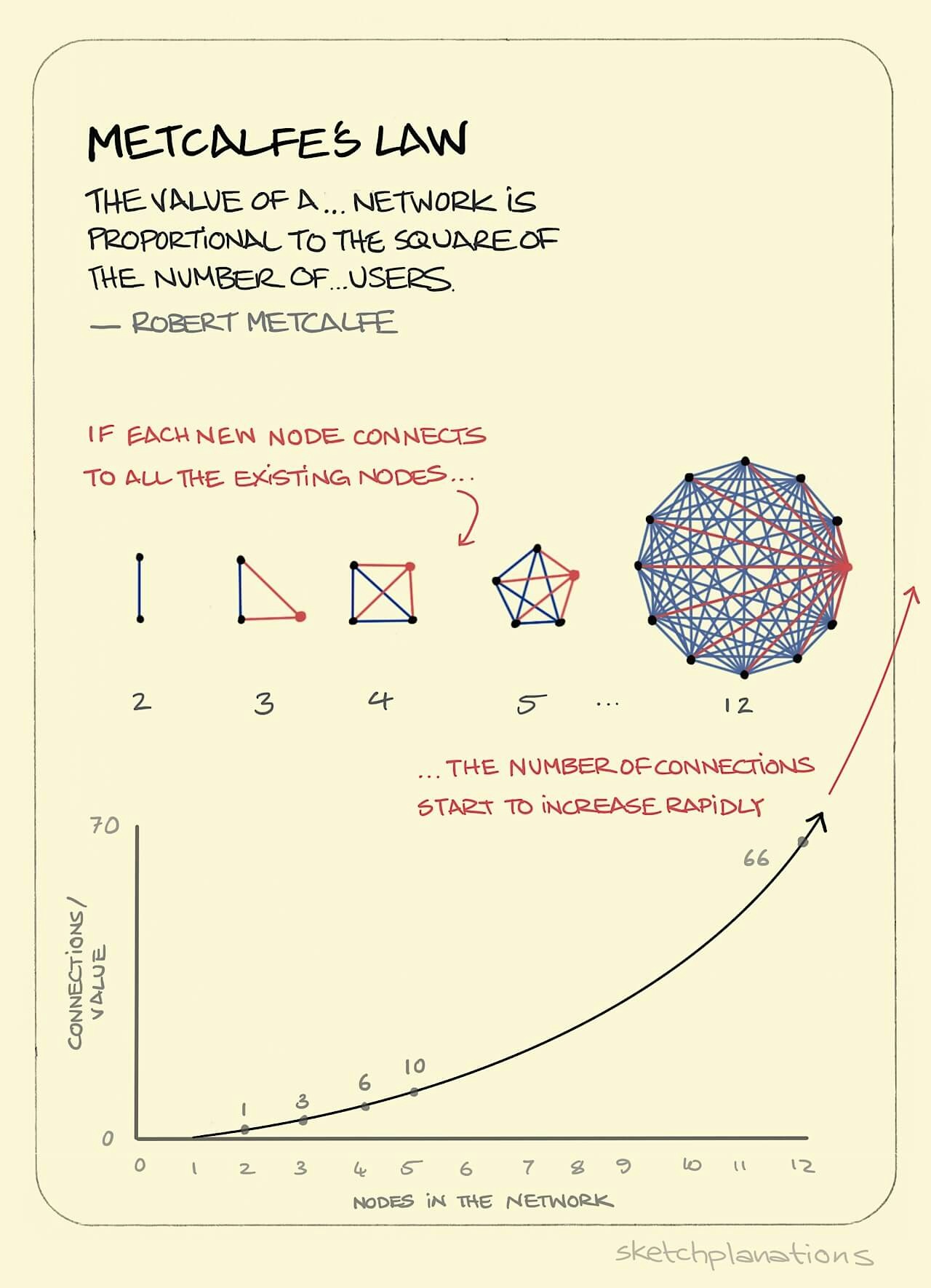
Metcalfe's Law is: "The value of a telecommunications network is proportional to the square of the number of users of the system."
— Robert Metcalfe
This law explains a little of the remarkable power of a growing network. Each time you add a user or node to the network, the number of connections increases in proportion to the square of the number of users. So, in this simple example where every new node gets a connection to each of the existing nodes, you can see that, say, adding a single node to an 11-node network creates 11 new connections.
It’s a simplified example because in most networks, the value is not directly proportional to the number of connections as some connections or users may be more valuable than others, and usually, adding a new user wouldn’t create a connection to all existing users — say if it was in a different country, or people spoke a different language or just cared about different things. But nevertheless, you can see how a network quickly becomes valuable as users join.
So, Facebook has about 2 billion users…
Metcalfe was talking about telecommunications networks, and the basic proposition has been modified since it was formulated, including by Metcalfe himself.
Just because something is called a law doesn’t mean it is one. See
