Binary
👇 Get new sketches each week
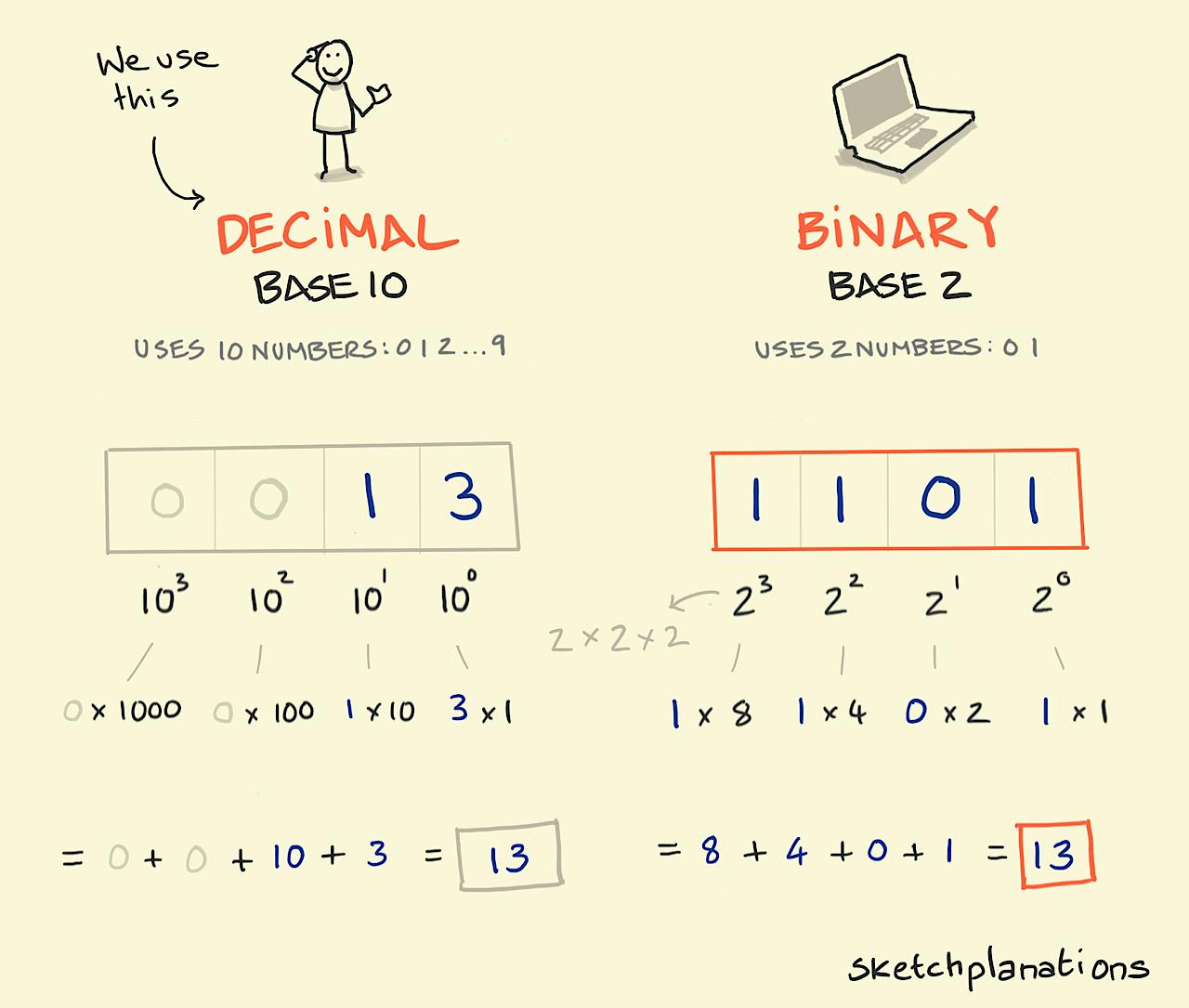
We find it handy to count in the decimal system using 10 numbers from 0,9, known as base 10, before we have to put two together to make 10 to keep counting further — 10 fingers and toes and all. But it turns out you can represent all numbers equally using just two digits, known as base 2, a 0 and a 1. This is called the binary system and is credited to Gottfried Wilhelm Liebniz in the 1600s.
The binary system is handy because 1s and 0s can be represented by simply by on/off and reproduced in as simple means as pebbles in trays , the sign of a magnetic field eg positive/negative, or a gate as open or closed. This made them the choice for designing computers and is how digital information is stored and transmitted today.
When we write a decimal number we use positional notation with each successive position representing 10 to the next power. So 739 is understood as (7 x 10^2) + (3 x 10^1) + (9 x 10^0). 10 to the power 2 is 10 x 10, so is the number of 100s in the number. Anything to the power 0 is 1.
The same is true in binary, so 1101 is understood in decimal as:
1101 = (1 x 2^3) + (1 x 2^2) + (0 x 2^1) + (1 x 2^0)
or
1101 = (1 x 8) + (1 x 4) + (0 x 2) + (1 x 1)
= 8 + 4 + 0 + 1
= 13Each 0 or 1 in a binary number is known as a bit — named by Claude Shannon as short for binary digit — and 8 bits is known as a byte.
Translating to decimal looks fiddly, but computers don't have to do that, they can just add, subtract or multiply the binary numbers directly. Amazing to think that the device you may be reading this on now is just incredibly efficient at manipulating 1s and 0s.
For a readable and visual introduction to the history and operation of computers — from binary, logic gates, transistors, circuits, and Moore's law through to software and AI — you could do a lot worse than my Dad's book The Computing Universe 😀

